Pythagoras on the fresco "The School of Athens" by Raphael Sanzio

Raphael's Masterpieces

Raphael ->main page

Pythagoras

The Pythagorean Harmonic Scale

Who is located near Pythagoras?

Pythagoras Bio

Pythagoras is represented by his theory of mathematical harmony

Raphael Santi
Pythagoras
and Musical Proportion
on the fresco "The School of Athens"
(enlarged)
1509-1511
Vaticano, Stanza della Segnatura, Rome

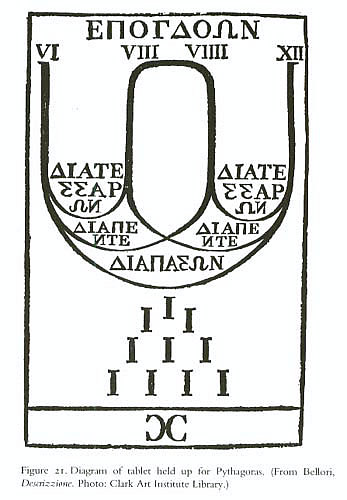
Youth holds at the feet of Pythagoras a panel on which is inscribed his consonances of song. Pythagoras saw in the geometry of musical harmony a key to the order of the cosmos ("harmony of the spheres"). Notice the tablet. It shows: the words diatessaron, diapente, diapason. The roman numerals for 6, 8, 9, and 12, showing the ratio of the intervals, same as in the music book frontispiece. Under the tablet is a triangular number 10 called the sacred tetractys.

Pythagoras is represented by his theory of mathematical harmony on the left, Euclid by the perfection of Geometry on the right -- and the elaborate perspective design of the architectural setting seems to embody both. Pythagoras [and not the Evangelist Matthew according to Vasari in the 16th c. Pythagoras, representing Arithmetic, is sitting in the foreground. The two men who are jostling to look over his shoulder recall figures in Leonardo da Vinci's unfinished Adoration of the Magi in the Uffizi. Raphael had occasion to study Leonardo's picture during his stay in Florence. Probably Raphael used two Groups (one around Pythagoras) to show some early Philosophers with the somehow mysterious Pythagoras and the other group around Euclid (or Archimedes), Ptolemy etc. who represent more the clear true Science. A closer look at Pythagoras text, we recognize his most important discovery of harmony theory (music) and the numbers 1, 2, 3 and 4 which added together give the sacred number 10 (X). Epogdoon is a natural number which is 1/8 larger than a given number for example 18 is the Epogdoon of 16.

The Pythagorean Harmonic Scale, tone, diatessaron, diapente, diapason

Take four pieces of string 6", 8", 9", 12", of equal consistency, and vibrate them under equal tension

interval between VI (6) and XII (12)
= octave

interval between VI (6), IX (9), and between VIII (8) and XII (12)
= fifth

interval between VI (6) and VIII (8), and between IX (9) and XII (12)
= fourth

interval between VIII (8) and IX (9)
= major tone

Under Raphael's musical diagram is a representation a triangular figure composed of 4 rows of 10 points: I, II, III, IIII, called the tetractys, which is the Pythagorean perfect number 10. The sum of the first four figures constitutes all musical harmonies. Moreover, the Pythagorean number 10 comprises all numbers, and thus was regarded as sacred and as the "mother of the universe."

As can be seen from the tablet, 10 is the sum of the first four figures (1, 2, 3, 4) which constitutes all musical harmonies and can be associated with the philosophical concept of the Harmony of the Spheres.

In harmony, diapason is the ratio of 2:1 between a pair of frequencies . The diapason is also called octave. The diatessaron is a ratio of 4:3 between a pair of frequencies. It is the harmonic mean of unison and diapason: Diapente is the ratio 3:2 between a pair of frequencies or, equivalently, the ratio 2:3 between a pair of wavelengths. It is the arithmetic mean of diapason and unison. In a diagrammatic representation of a lyra the strings are tuned in the relative proportions VI, VIII, VIIII, XII giving the intervals of an octave (diapason) between VI and XII, fifths (diapente) between VI, VIIII and VII, XII and fourths (diatessaron) between VI, VIII and VIIII, XII. The interval of a tone is present between VIII and VIIII. In contrast to the group around Euclid (or Archimedes) persons around Pythagoras stretch their head to see what Pythagoras is writing.

Drawing Steps:
From paper...	...to cardboard...	...to the final fresco.

Who is located near Pythagoras?

Who is the old man who copies the words of Pythagoras? Probably Boethius [Anicius Manlius Severinus Boethius (480 Rome – c. 524-526 execution of Boethius)], a person who with his work was influential in the Medieval times, with books such as Consolatio Philosophiae (The Consolation of Philosophy) written when he was in prison before his execution. Due to his knowledge of Greek he translated various astronomical and mathematical Greek texts which were important for the advance of Science in Europe.
Some say it is Empedocles, Zeno, Archytas of Tarentum, Iamblichus. But maybe also Anaximander (611 - 547 BC) (there are some similarities of this image with a sculpture of Anaximander), Terpander or Nicomachus or another musician and follower of Pythagoras.

The philosopher of Cordoba Averroës [Abu Al-Walid Muhammad Ibn Ahmad Ibn Muhammad Ibn Ahmad Ibn Ahmad Ibn Rushd (1126 Cordoba - 10.12.1198 Marrakech /Morocco)] identified by his turban. He was an author with commentaries to Aristotle's Metaphysics and On The Soul, Commentaries to Plato's Republic and many more other books about Philosophy, Astronomy, Medicine.

Pythagoras
Greek philosopher and mathematician

Pythagoras, (born c. 570 bce, Samos, Ionia [Greece]—died c. 500–490 bce, Metapontum, Lucanium [Italy]) Greek philosopher, mathematician, and founder of the Pythagorean brotherhood that, although religious in nature, formulated principles that influenced the thought of Plato and Aristotle and contributed to the development of mathematics and Western rational philosophy. (For a fuller treatment of Pythagoras and Pythagorean thought, see Pythagoreanism).

Pythagoras emigrated to southern Italy about 532 bce, apparently to escape Samos’s tyrannical rule, and established his ethico-political academy at Croton (now Crotone, Italy). It is difficult to distinguish Pythagoras’s teachings from those of his disciples. None of his writings have survived, and Pythagoreans invariably supported their doctrines by indiscriminately citing their master’s authority. Pythagoras, however, is generally credited with the theory of the functional significance of numbers in the objective world and in music.

Other discoveries often attributed to him (the incommensurability of the side and diagonal of a square, for example, and the Pythagorean theorem for right triangles) were probably developed only later by the Pythagorean school. More probably, the bulk of the intellectual tradition originating with Pythagoras himself belongs to mystical wisdom rather than to scientific scholarship.
Encyclopædia Britannica, Inc.

	Back to Raphael-main page

	The School of Athens

ABC-People Home Page